프로그래머스 디스크 컨트롤러

https://programmers.co.kr/learn/courses/30/lessons/42627

코딩테스트 연습 - 디스크 컨트롤러

 

음... 난 이런 류의 문제에 약한걸까.. 

 

진정한 뇌정지가 와서 아예 모르겠었다.. 어떻게든 다른분의 풀이를 참고하지 않고 풀어보려고 했으나 한번 막힌 머리는 돌아갈줄을 몰랐다..

 

이런 문제를 한번씩 접할때마다 좌절스럽다 

 

그래도 어쨌든.. 풀이를 보고 어떻게 해야하는지 이해하였다. 앞으로 이런 유형의 문제를 또 만났을 때 풀어낼 수 있도록 확실히 이해하고 비슷한 유형의 문제도 많이 풀어봐야겠다.

 

 

이 문제의 풀이는 아래와 같다.

 

1. 디스크가 작업을 수행할 수 있는 탐색범위를 초기화한다.

- 현재까지 수행완료된 ms 를 초기화한다. (now)

- 시작 범위를 초기화한다 (start)

2. 큐에 시작범위부터 수행완료된 ms 범위내에 job이 있으면 작업 우선순위큐(work_q)에 담는다.

3. 작업우선순위 큐에 담을때 작업수행시간을 짧은 것을 먼저 수행해야만 대기시간이 짧아지므로 작업수행시간을 첫번째 요소로 담는다.

4. 작업큐에 값이 있으면 작업시간이 가장 짧은 것을 꺼낸다(pop)

5. 탐색범위를 변경한다. (작업큐에 값이 없으면 현재시점, 즉 탐색범위를 1 증가시킨다)

 

6. 요청부터 종료까지의 소요시간을 누적한다.

7. 수행완료된 횟수를 +1 증가시킨다.

 

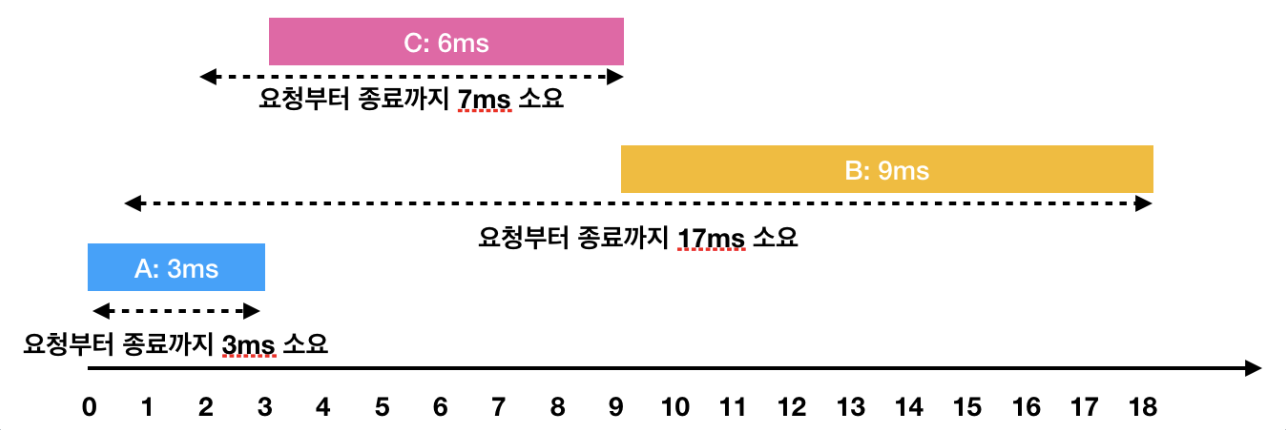
초기 탐색범위는 start 가 -1 now가 0 이였으므로

작업 요청 시점이 -1,0 사이인 작업이 있으면 work_q 에 담는다.

위 예의 경우엔 (0,3) 이 담긴다.

 

(0,3) 을 처리하면서 start = 0 으로 now = 3 (0+3) 으로 변경된다.

작업 시간을 누적한다. 작업 시간은 현재까지 누적된 작업소요시간에 작업 요청시간을 빼주면 된다. (위 이미지에서 요청부터 종료까지 3ms 소요 라고 표시된 부분)

수행완료된 작업(complete_job)을 1 추가한다 

 

다음 순환에선 작업 요청 시점이 0 부터 3 사이인 작업을 탐색한다.

 

(2, 6), (1, 9) 가 담긴다.

(2,6) 을 처리하면서 (작업소요시간이 최소인 것을 pop 하므로 2,6 이 1,9 보다 먼저 수행된다) start = 3 으로 now = 9 (3+6) 으로 변경된다.

작업 시간을 누적한다. 작업 시간은 현재까지 누적된 작업소요시간에 작업 요청시간을 빼주면 된다. (9-2=7 위이미지에서 요청부터 종료까지 7ms 라고 표시된 부분)

 

다음 순환에선 작업 요청 시점이 3 부터 9 사이인 작업을 탐색한다.

추가로 담을 작업은 없다.

 

하지만 work_q 에는 처리할 작업이 남아있다. 

(1,9)를 위와같은 방식으로 처리한다.

 

1,9 를 처리하면 complete_job 이 전체 작업(len(jobs))  와 같아지므로 루프를 종료한다.

 

최종 누적된 소요시간에 총 작업 수를 나누면 정답이다.

 

 

 

import heapq


def solution(jobs):
    ans = 0
    start = -1
    now = 0
    complete_job = 0
    work_q = []
    while complete_job < len(jobs):
        for job in jobs:
            if start < job[0] <= now:
                heapq.heappush(work_q, [job[1], job[0]])

        if work_q:
            cur_job = heapq.heappop(work_q)
            start = now
            now += cur_job[0]
            ans += now - cur_job[1]
            complete_job += 1
        else:
            now += 1

    return ans // len(jobs)


print(solution([[0, 50], [1, 1], [2, 2]]))

# [[0, 3], [1, 9], [2, 6]]	9
# print(solution([[0, 3], [1, 9], [2, 6]]))               # 9
# print(solution([[0, 3], [4, 3], [10, 3]]))              # 3
# print(solution([[0, 10], [2, 3], [9, 3]]))              # 9
# print(solution([[1, 10], [3, 3], [10, 3]]))             # 9
# print(solution([[0, 10]]))                              # 10
# print(solution([[0, 10], [4, 10], [5, 11], [15, 2]]))   # 15
# print(solution([[24, 10], [18, 39], [34, 20], [37, 5], [47, 22], [20, 47], [15, 2], [15, 34], [35, 43], [26, 1]]))   # 74